赛马问题

赛马问题：25匹马，5条赛道，每个跑道最多能有1匹马进行比赛，只能记录比较的名次信息，求最少赛多少次即可得出前五名？

先说结论：采用合适的策略，最坏比赛8次即可得到跑的最快的前五名。

虽然网上有很多分析，但是大多都是最坏要比较9次或10次的方案，并不够完善，我这里提供一个比较完整的分析。

Step 1

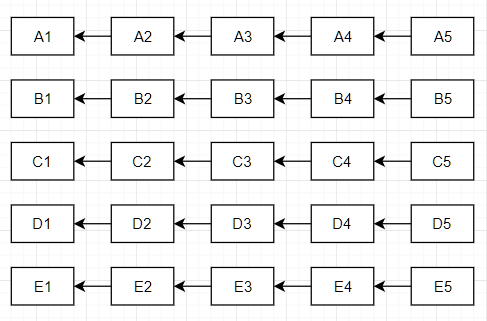
分成五组进行比赛，不妨设分别为A，B，C，D，E 五组。

每个马匹编号为$ A_i,i {1,2,3,4,5}$, \(A_i\) 代表这匹马在A组中名次为 \(i\) .

比赛结果如下 :（箭头指示快慢顺序）

Step 2

这一步比较关键，网上流传的答案大多是把 所有跑第一的马（即A1,B1,C1,D1,E1）拉出来比较.而实际上把所所有跑第二的马 拉出来比较是更好的选择。选第二名进行比较的好处在于可以排除14匹马，而选第一名只能排除10匹马。

如果比较跑第一的马，那么得到的结果是这样的：

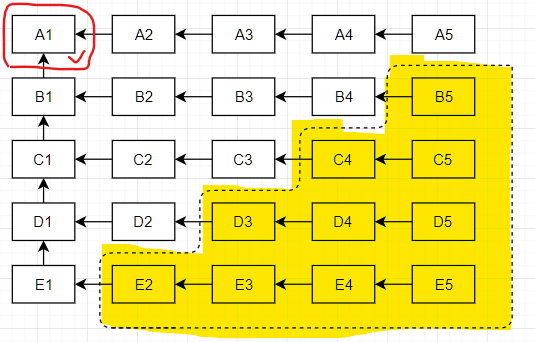
虚线包围的黄色区域是被排除的不可能进前五的马

红线圈出的马A1则是唯一确定进前五并且为所有马中跑的最快的马。

如果比较跑第二的马，得到的结果如下：

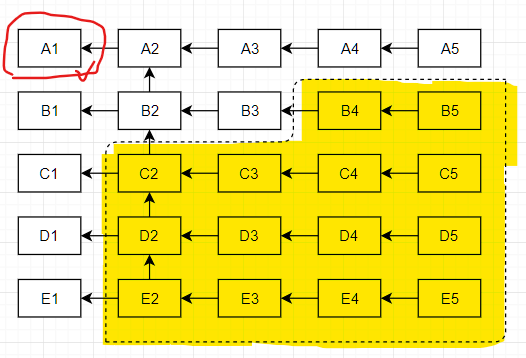
明显排除了更多的马

Step 3

完成第一步和第二步后，我们已经比较了6次，只需要在不确定的10匹马中找出前四即可完成任务。

而这一步比较的方案是一个估计出的结果，在这一步中将 A3, B2, C1, D1, E1 拉出来进行比较即可。

我们着重以B2和A3的名次进行分情况讨论：

好吧，这里讨论挺复杂的。。。但是只要分析一下就可以得出（最多再额外比较两次即可选出前五）的结论。

结论

重点在于第二步中，选取合适的马比较以排除最多数量的马（类似二分搜索的思想）