RL学习笔记01
Reinforcement learning
分类
- model-free and model-based
- policy-based and value-based
- Monte-Carlo update and Temporal-Difference update
- On-policy and Off-policy
chart
| Q learning | Policy Gradients (base) | Sarsa | Actor-Critic | Monte-carlo learning | policy gradients (upgrade) | Sarsa (lambda) | DQN |
|---|---|---|---|---|---|---|---|
| value-based | policy-based | value-based | both | value-based | value-based | ||
| TD | MC | TD | MC | TD | |||
| Off-policy | On-policy | On-policy | Off-policy | ||||
| s,a,s' | s,a,s',a' | s,a,s',a' | s,a,s' |
algorithm
Q learning

- Q(s,a) 存储某个state下所有可能action的value. $size = state_dim action_dim $
- 更新时 利用学习的历史来提供远见,\(\alpha\) 为学习率,后面中括号内为新的现实(中间夹杂有远见)与当前学习到的估计的差距.
- 由此可见,为单步更新, 可以修改为off-policy
- $$ 代表了远见的权重
Sarsa

- . 因为 Sarsa 是说到做到型, 所以我们也叫他 on-policy, 在线学习, 学着自己在做的事情. 而 Q learning 是说到但并不一定做到, 所以它也叫作 Off-policy, 离线学习.
- 和Q learning 的区别
- 同样的在某一个state,采用 \(\epsilon - greedy\) 选择下一个动作action, 然后去做 观察到新的state
- 不同的是,Q learning 更新Q value 使用的是\(maxQ\) 选出的action, 而Sarsa使用的是 \(\epsilon - greedy\) 选出的实际上下一步要采取的动作action.
- 因此Q learning 是off-policy, 因为它更新Q value 所用的action,它不需要去做. 因此可以用打乱顺序的state加上对应的action学习
- 而Sarsa不同,是 On-policy,因为它更新Q value所用的action, 它一定要去做,因此state不能打乱,而且很容易和其它agent的学习经历冲突(因为action 具有一定的随机性,很难找到对应的state)
- 系数为\(\gamma\)的一项代表了agent的远见所能看到的东西
.
- Sarsa
由于预知时采用了部分随机的动作,因此不仅能看到最好的结果也能看到相邻可能遇到的危险,因此比较保守
- Q learning 只会看到最好结果,而不会看到危险,因此十分勇敢
- Sarsa
由于预知时采用了部分随机的动作,因此不仅能看到最好的结果也能看到相邻可能遇到的危险,因此比较保守
Sarsa(lambda)
i.e. Sarsa(\(\lambda\))
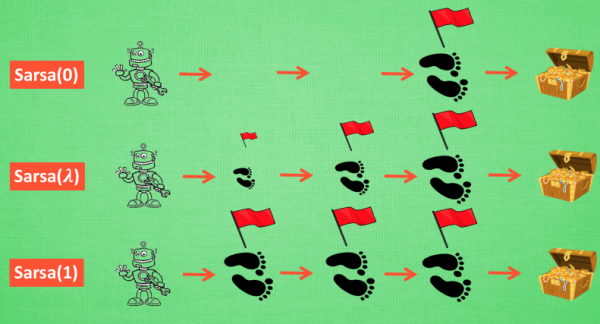
- relative introduction

- 从上图可以看出,和Sarsa相比,Sarsa(lambda)算法中多了一个矩阵E (eligibility trace),它是用来保存在路径中所经历的每一步,因此在每次更新时也会对之前经历的步进行更新。
- 参数lambda取值范围为[0, 1] ,如果 lambda = 0,Sarsa(lambda) 将退化为Sarsa,即只更新获取到 reward 前经历的最后一步;如果 lambda = 1,Sarsa(lambda) 更新的是获取到 reward 前的所有步。lambda 可理解为脚步的衰变值,即离奶酪越近的步越重要,越远的步则对于获取奶酪不是太重要。
- Sarsa虽然会边走边更新,但是在没有获得奶酪之前,当前步的Q值是没有任何变化的,直到获取奶酪后,才会对获取奶酪的前一步更新,而之前为了获取奶酪所走的所有步都被认为和获取奶酪没关系。Sarsa(lambda)则会对获取奶酪所走的步都进行更新,离奶酪越近的步越重要,越远的则越不重要(由参数lambda控制衰减幅度)。因此,Sarsa(lambda) 能够更加快速有效的学到最优的policy。
- 在算法前几回合,老鼠由于没有头绪, 可能在原地打转了很久,从而形成一些重复的环路,而这些环路对于算法的学习没有太大必要。Sarsa(lambda)则可解决该问题,具体做法是:在E(s,a)←E(s,a)+1这一步之前,可先令E(s)=0,即把状态s对应的行置为0,这样就只保留了最近一次到达状态s时所做的action。
DQN
state 过多,所以使用NN来计算Q value。有两种方法
- \(state + action \rightarrow action\_value\)
- \(state \overset{NN}{\rightarrow}\left\{ \begin{aligned} &action1 \_ value \\ &action2 \_ value \\ &...\end{aligned} \right.\)
NN 的更新:
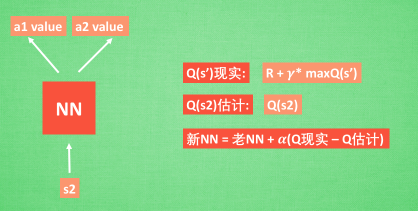
利用指定的state和action进行更新,即当前状态和选择的动作。新的state已经确定但是新的action并不确定。
two tricks
- Experience replay (Q learning off-policy 的特性)
- Fixed Q-targets 利用很久以前的参数为行为策略更新

Policy Gradients
- link
- Policy network 输出的是动作或者动作概率 而DQN 输出的是价值,本质上是接近于确定性输出的算法
- 没有LOSS的network!!!
- 如何更新? 增大得到好结果动作的概率,减小得到坏结果动作的概率
- 难点,如何对动作进行评价
- 进一步研究link
- 概览

- code link
Actor Critic
Policy Gradients + Q learning
环境的reward 指导 Critic(Q learning) 更新,Critic 再根据历史学习的Q value 来指导 Actor的更新
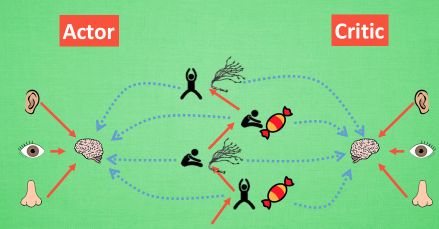
但是连续状态更新,导致神经网络学不到东西
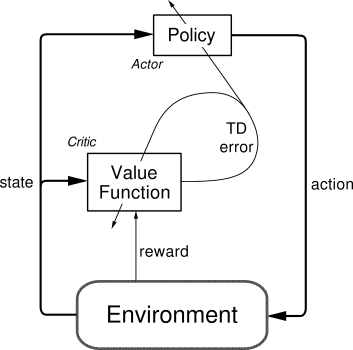
- 改进版 Deep Deterministic Policy Gradient (DDPG)
- Actor-Critic + DQN